지난 블로그에는 GD, SGD, Momentum, Adagrad 관련 내용에 대해서 설명 했습니다.
이번에는 현재(2024년 기준) 많이 쓰이는 Adam 에 대해서 작성해보겠습니다.
모델을 학습할때 그냥 일반적으로 Adam 을 사용한다고 하는데 왜 그런지 이번에 알고자 작성했습니다.
RMSProp ,Adam, AdamW, AdamP 4가지에 대해서 알아보자.
1. RMSProp (Root Mean Square Propagation)
RMSProp는 AdaGrad의 단점인 학습률 감소 문제를 해결하기 위해 개발된 알고리즘이다.
AdaGrad는 기울기의 제곱값을 누적하여 학습률을 조정하지만, 이 누적값이 너무 커지면 학습률이 지나치게 작아져 학습이 멈추는 문제가 발생한다. RMSProp는 이러한 문제를 해결하기 위해 기울기 제곱값의 지수 이동 평균(Exponential Moving Average)을 사용한다.
1. 기울기 제곱값의 이동 평균 계산
- \( E[g^2]_t = \beta E[g^2]_{t-1} + (1 - \beta) g_t^2 \)
\( E[g^2]_t \) : 기울기 제곱값의 지수 이동 평균
\( \beta \) : 지수 이동 평균을 조절하는 계수(일반적으로 0.9)
\( g_t \) : 현재 기울기
수식을 쉽게 얘기하면,
과거 정보 ( \( E[g^2]_t \) ) 는 축적된 기울기 제곱값의 평균을 나타내고,
현재 정보 ( \( g_t^2 \) ) 는 현재 단계에서의 기울기 크기를 나타낸다.
직관적으로 얘기해보면,
"기울기가 얼마나 큰지"를 계산해서 학습률에 반영하려고 하고,
과거 값과 현재 값을 적절히 섞어서 너무 과거에 치우치지도, 현재에 치우치지도 않게 하려고 하는것 이다.
2. 가중치 업데이트
- \( w_{t+1} = w_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \cdot g_t \)
: 학습률
\( \epsilon \) : 안정성을 위한 작은 값(분모가 0이 되는 것을 방지)
수식을 쉽게 애기하면,
학습률을 적응적으로 조정하여 가중치를 업데이트 한다.
기울기가 자주 커지는(변화가 큰) 파라미터는 학습률을 줄여 더 작은 폭으로 업데이트
기울기가 작은(변화가 적은) 파라미터는 학습률을 키워 더 큰 폭으로 업데이트
직관적으로 얘기해보면,
"기울기가 너무 큰 곳은 천천히 움직이고, 기울기가 작은 곳은 더 많이 움직이자"라는 접근 방식이다.
이렇게 하면 효율적이고 안정적으로 최적점을 찾아갈 수 있다.
더 직관적으로 비유를 통해서 한번 더 이해해보자.
물을 따라 내려가는 공
- : 언덕에서 굴러가는 공의 위치
- : 공이 있는 언덕의 경사도(기울기의 크기)
- \( E[g^2]_t \) : 과거 경사도 정보를 기반으로 한 현재 경사도의 "평균 경사도"
- \( \eta \) : 공이 굴러가는 속도(학습률)
RMSProp가 하는 일
- 공이 경사가 매우 급한 곳(기울기가 큰 곳)에서는:
- \( E[g^2]_t \) 값이 커지므로, 공의 속도 \( \frac{\eta}{\sqrt{E[g^2]_t}} \) 를 낮춰 천천히 움직이게 한다.
- 공이 너무 빠르게 내려와 최적점을 지나쳐버리지 않도록 조절
- 경사가 완만한 곳(기울기가 작은 곳)에서는:
- \( E[g^2]_t \) 값이 작아져 공의 속도가 더 빨라지게 한다
- 공이 멈춰버리지 않고 계속 움직일 수 있도록 도와준다.
즉,
RMSProp는 경사하강법에서 공이 너무 빠르게 움직이거나, 너무 느려져 멈춰버리는 것을 방지하며,
언덕의 경사도에 따라 공이 굴러가는 속도를 적응적으로 조절하면서, 최적점을 향해 안정적으로 이동한다.
RMSProp의 단점
RMSProp는 \( \beta \) (기울기 제곱값의 지수 이동 평균 계수)와 \( \eta \) (학습률) 두 개의 중요한 매개변수를 필요로 한다. 2개의 잘못된 설정은 학습 효율에 큰 영향을 미친다.
- 가 너무 크면: 과거 정보에 지나치게 의존하여 현재 기울기의 영향을 적게 받아 학습 속도가 느려질 수 있다
- β가 너무 작으면: 과거 정보를 거의 무시하고, 기울기의 노이즈가 증가해 학습이 불안정해질 수 있다.
- 학습률이 너무 크면: 최적점에서 발산할 수 있고,
- 학습률이 너무 작으면: 학습이 지나치게 느려질 수 있다.
이러한 단점을 보완하기 위해 Adam 이 나왔다
2. Adam (Adaptive Moment Estimation)
Adam은 Momentum과 RMSProp의 아이디어를 결합하여 개발된 알고리즘이다.
Momentum을 사용해 기울기의 이동 평균(1차 모멘트)을 계산하고, RMSProp의 방식으로 기울기 제곱값의 이동 평균(2차 모멘트)을 계산한다. 이를 통해 빠른 수렴과 적응형 학습률 조정이라는 두 가지 장점을 모두 갖춘다.
1차 모멘트(평균) 계산
\(
m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t
\)
1차 모멘트는 기울기(\( g_t \))의 지수 이동 평균(Exponential Moving Average)을 계산한 값이다.
- : 현재 기울기의 이동 평균이다.
- β1 : 이전 값( \( m_t-1 \) )에 얼마나 의존할지를 결정하는 계수이다. 일반적으로 β1=0.9로 설정한다.
- : 현재 단계에서의 기울기(Gradient)이다.
이 단계에서 과거 기울기와 현재 기울기를 적절히 혼합하여 기울기의 평균적인 방향을 계산한다.
이는 학습을 안정적으로 진행하기 위해 기울기의 진동(Noise)을 줄이는 역할을 한다.
2차 모멘트(분산) 계산
\(
v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2
\)
2차 모멘트는 기울기의 제곱값의 지수 이동 평균을 계산한 값이다.
- \( v_t \) : 기울기의 제곱값에 대한 이동 평균이다.
- β2 : 이전 값 \( v_t-1 \) 에 얼마나 의존할지를 결정하는 계수이다. 일반적으로 β2=0.999로 설정한다.
- : 현재 단계에서 기울기의 제곱값이다.
2차 모멘트는 기울기 크기의 변화를 추적하여, 학습률을 조정하는 데 사용된다.
즉, 기울기가 큰 경우에는 학습률을 작게, 기울기가 작은 경우에는 학습률을 크게 한다.
바이어스 보정
\(
\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}
\)
Adam은 초기 단계에서 1차 모멘트와 2차 모멘트가 0으로 편향(Bias) 되는 문제를 해결하기 위해 바이어스 보정을 적용한다.
- : 바이어스가 보정된 1차 모멘트이다.
- : 바이어스가 보정된 2차 모멘트이다.
- t: 현재 반복(epoch) 횟수이다.
이 과정은 학습 초기에 \( \hat{m}_t \) 와 \( \hat{v}_t \) 값이 0에 가까운 값으로 시작되기 때문에, 이를 보정해 실제 기울기를 더 정확하게 반영하도록 한다.
가중치 업데이트
\(
w_{t+1} = w_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \cdot \hat{m}_t
\)
가중치 업데이트는 바이어스가 보정된 1차 및 2차 모멘트를 기반으로 이루어진다.
- : 현재 가중치이다.
- : 업데이트된 가중치이다.
- η : 학습률(Learning Rate)이다.
- : 바이어스가 보정된 기울기의 평균 방향(1차 모멘트)이다.
- \( \hat{v}_t \) : 바이어스가 보정된 기울기의 크기(2차 모멘트)이다.
- ϵ: 안정성을 위해 추가된 작은 값이다. 일반적으로 \(10^{-8}\) 로 설정한다.
이 식은 기울기의 방향과 크기를 모두 고려하여 학습률을 적응적으로 조정한다.
- 기울기가 크면 \(\sqrt{\hat{v}_t}\) 값이 커져 학습률이 작아지고,
- 기울기가 작으면 학습률이 커지면서 더 많이 이동한다.
식은 직관적으로 이해하기 어려우니 다른 비유로 설명을 하면,
Adam은 물리적인 관성과 적응형 조정을 결합한 방식이다. 이를 공을 언덕에서 굴리는 상황에 비유할 수 있다.
- : 공이 움직이는 방향(기울기의 평균적인 방향).
- : 공이 움직이는 속도의 크기(기울기의 크기에 따른 이동량 조정).
- 바이어스 보정: 초기의 불안정한 움직임을 보정해주어 더 정확한 방향으로 공이 굴러가게 한다.
Adam은 기울기의 방향을 안정적으로 추적하면서, 경사가 급한 곳에서는 천천히 이동하고 경사가 완만한 곳에서는 더 빠르게 이동하여 최적점을 향해 효율적으로 이동할 수 있게 한다.
비유를 통한 Adam 이해
위에 식은 어찌어찌 이해하겠는데...
왜 저렇게 하는지 그리고 머릿속에 기억에 남도록 다른 비유로 이해해보자
Adam을 자동차가 산길을 내려가는 상황으로 생각해보자.
- 목표: 자동차가 안전하고 효율적으로 최적의 위치(산 아래의 목적지)로 도달하는 것
- 문제: 경사도가 급격히 변하거나(산길), 도로의 상태(손실 함수 곡률)가 고르지 않아서 주행이 어렵다.
Adam은 다음과 같은 두 가지 전략을 통해 최적의 위치로 안정적으로 이동한다.
- 방향과 관성 유지: 이전 이동 방향을 활용하여 움직임을 더 부드럽게(모멘텀 기반)
- 속도 조절: 도로 상황(기울기 크기)에 따라 속도를 조절해 과속하거나 멈추지 않도록 한다(적응형 학습률)
1차 모멘트 ( \( m_t \) ): 방향과 관성을 활용해 부드럽게 움직인다.
\(
m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t
\)
비유
- \( m_t \) 는 자동차의 현재 방향과 속도를 결정한다.
- 자동차가 급격히 방향을 바꾸는 것은 위험하다. 그래서 Adam은 이전의 방향 \( m_t-1 \) 을 참고하면서, 현재의 상황 \( g_t \) 도 반영한다.
- β1는 관성을 얼마나 유지할지 결정한다. 보통 0.9로 설정해, 이전 방향의 영향을 더 많이 반영하도록 한다.
왜 필요한가?
- 기울기 \( g_t \) 만을 그대로 따라가면 경사면이 급변할 때 진동(Oscillation)이 발생할 수 있다.
- 관성을 활용하면, 진동을 줄이고 움직임이 더 부드럽고 안정적이 된다.
2차 모멘트 \( v_t \) : 도로 상황에 따라 속도를 조절한다
\(
v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2
\)
비유
- \( v_t \) 는 자동차의 도로 상태(경사도)의 평균적인 상태를 기록한 것이다.
- 도로가 급격히 경사진 구간(기울기 \( g^2_t \) 가 큰 경우)에서는 속도를 줄여야 사고를 방지할 수 있다.
- 반대로, 도로가 평탄한 구간(기울기 \( g^2_t \) 가 작은 경우)에서는 속도를 높여 빠르게 이동할 수 있다.
- β2는 도로의 과거 정보를 얼마나 신뢰할지를 결정한다.
왜 필요한가?
- 기울기가 큰 곳에서는 속도를 줄여 안정적으로 이동하고, 기울기가 작은 곳에서는 속도를 높여 효율성을 극대화하기 위해 필요하다.
바이어스 보정: 초기 이동을 정확하게 한다
\(
\hat{m}_t = \frac{m_t}{1 - \beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1 - \beta_2^t}
\)
비유:
- 초기 단계에서는 자동차가 출발한 지 얼마 되지 않았기 때문에, 방향 \( m_t \) 과 속도 \( v_t \) 정보가 충분히 쌓이지 않았다.
- Adam은 이를 보정하여 초기 이동이 너무 느리거나 잘못된 방향으로 가는 문제를 방지한다.
왜 필요한가?:
- 기울기의 평균과 분산 계산은 초기에 편향되기 쉽다. 바이어스 보정을 통해 초기 이동도 정확하게 반영할 수 있도록 한다.
가중치 업데이트: 속도와 방향을 조합하여 안전하게 이동한다
\(
w_{t+1} = w_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \cdot \hat{m}_t
\)
비유:
- : 현재 자동차의 위치.
- \( \hat{m}_t \) : 이동해야 할 방향(현재의 평균 기울기 방향).
- : 속도를 조절하는 기준(도로의 경사도 크기).
- ϵ: 도로 상태가 너무 평탄할 때 속도가 멈추지 않도록 추가하는 안전장치.
Adam은 \( m_t \)를 기반으로 방향을 잡고, \( v_t \)를 기반으로 속도를 조절하며 가중치(위치)를 업데이트한다.
- 경사가 큰 곳에서는 속도를 줄여 안정적으로 이동하고, 경사가 평탄한 곳에서는 속도를 높여 빠르게 이동한다.
왜 Adam이 효과적인가?
- 관성 효과
- 이전 방향을 유지하면서 기울기의 노이즈를 줄이기 때문에, 더 부드럽고 안정적인 이동이 가능하다.
- 속도 조절
- 도로의 상태(기울기 크기)에 따라 속도를 적응적으로 조절하여 효율성과 안정성을 모두 확보한다.
- 초기 안정성
- 초기 단계에서 바이어스 보정을 통해 학습이 너무 느리거나 방향을 잘못 잡는 문제를 방지한다.
Adam은 마치 스마트한 자율주행 자동차와 같다.
- 이전 이동 정보를 활용해 방향을 안정적으로 유지하면서,
- 도로의 경사도에 따라 속도를 조절하며 목적지에 효율적으로 도달한다.
- 초기 단계에서도 안정적으로 출발할 수 있도록 보정한다.
왜 일반적으로 Adam 을 사용하는 걸까?
안정적인 학습
기울기의 1차 모멘트(평균)와 2차 모멘트(분산)를 모두 사용하여 학습률을 조정한다.
- 1차 모멘트: 기울기의 평균 방향을 따라가 안정성을 유지
- 2차 모멘트: 기울기의 크기를 반영해 학습률을 조정(큰 기울기에서는 속도를 줄이고, 작은 기울기에서는 속도를 높임).
이러한 특성 덕분에 Adam은 손실 함수가 복잡하거나, 곡률이 급격히 변하는 상황에서도 안정적으로 수렴한다.
빠른 수렴
Adam은 일반적으로 SGD에 비해 수렴 속도가 빠르다.
- 1차 모멘트와 2차 모멘트를 동시에 사용하여 기울기의 방향과 크기를 적절히 조정하기 때문에, 초기 학습 속도가 빠르고 효과적이다.
- 특히, 데이터가 희소(sparse)하거나 손실 함수가 복잡한 경우, Adam이 더 빠르게 최적점을 향해 나아간다.
하지만 Adam 에도 단점은 있다.
학습률을 파라미터마다 자동으로 조정하는 특성상, 일부 파라미터에서 큰 업데이트가 발생할 수 있다.
이는 모델이 불필요하게 복잡해지고, 테스트 데이터에 대한 일반화 성능을 저하시킨다.
이러한 단점을 보완하기 위해 AdamW, AdamP 가 나왔다.
3. AdamW의 등장 이유
AdamW는 Weight Decay 문제를 해결하기 위해 등장했다.
- 문제
- Adam에서의 Weight Decay는 학습률 조정과 결합되어 불완전하게 작동한다.
- Weight Decay는 모델의 파라미터 크기를 제한하는 데 유용하지만, Adam의 경우 이는 단순히 Gradient에 더해지는 항으로 처리되어, 모델 파라미터 크기를 제대로 제한하지 못한다.
- 해결 방법 (AdamW)
- AdamW는 Weight Decay를 Gradient 업데이트와 분리하여 명확하게 구현했다.
- 가중치 감소를 모델 파라미터 자체에 직접 적용한다.
\[
w_{t+1} = w_t - \eta \cdot \left( \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} + \lambda w_t \right)
\]
- : Weight Decay 항으로, 모델 파라미터 크기를 제한한다.
- 장점:
- 일반화 성능 향상: 과적합을 줄이고 테스트 데이터에서 더 나은 성능을 보인다.
- Weight Decay와 학습률 조정이 분리되어, 의도한 대로 가중치 감소 효과를 적용할 수 있다.
AdamW는 Weight Decay와 학습률 조정 문제를 해결하여 일반화 성능을 개선하기 위해 등장했다.
4. 각각의 Optimizer 간단한 코드 실험
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torchvision.models import resnet18
import matplotlib.pyplot as plt
# CIFAR-10 데이터 로드
def load_data(batch_size=64):
transform = transforms.Compose([
transforms.Resize((32, 32)),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
train_dataset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
return train_loader
# 모델 초기화
def get_model():
model = resnet18(num_classes=10) # CIFAR-10 클래스 수 설정
return model
# 학습 함수
def train_model(optimizer_name, model, train_loader, criterion, device, epochs=10):
model.to(device)
# 옵티마이저 초기화
if optimizer_name == "RMSProp":
optimizer = optim.RMSprop(model.parameters(), lr=0.01, alpha=0.99)
elif optimizer_name == "Adam":
optimizer = optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999))
elif optimizer_name == "AdamW":
optimizer = optim.AdamW(model.parameters(), lr=0.001, betas=(0.9, 0.999))
else:
raise ValueError("Unsupported optimizer")
losses = []
for epoch in range(epochs):
model.train()
running_loss = 0.0
for inputs, targets in train_loader:
# 데이터를 GPU로 이동
inputs, targets = inputs.to(device), targets.to(device)
# 옵티마이저 초기화 및 학습 진행
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
running_loss += loss.item()
avg_loss = running_loss / len(train_loader)
losses.append(avg_loss)
print(f"Epoch {epoch+1}/{epochs}, {optimizer_name} Loss: {avg_loss:.4f}")
return losses
# Main 실행
def main():
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
train_loader = load_data()
criterion = nn.CrossEntropyLoss()
# 옵티마이저 목록 추가
optimizers = ["RMSProp", "Adam", "AdamW"]
results = {}
for optimizer_name in optimizers:
model = get_model()
print(f"\nTraining with {optimizer_name} optimizer...")
losses = train_model(optimizer_name, model, train_loader, criterion, device)
results[optimizer_name] = losses
# 결과 시각화
plt.figure(figsize=(10, 6))
for optimizer_name, losses in results.items():
plt.plot(range(1, len(losses) + 1), losses, label=optimizer_name)
plt.title("Loss Comparison of Optimizers")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()
plt.grid()
plt.show()
if __name__ == "__main__":
main()
결과
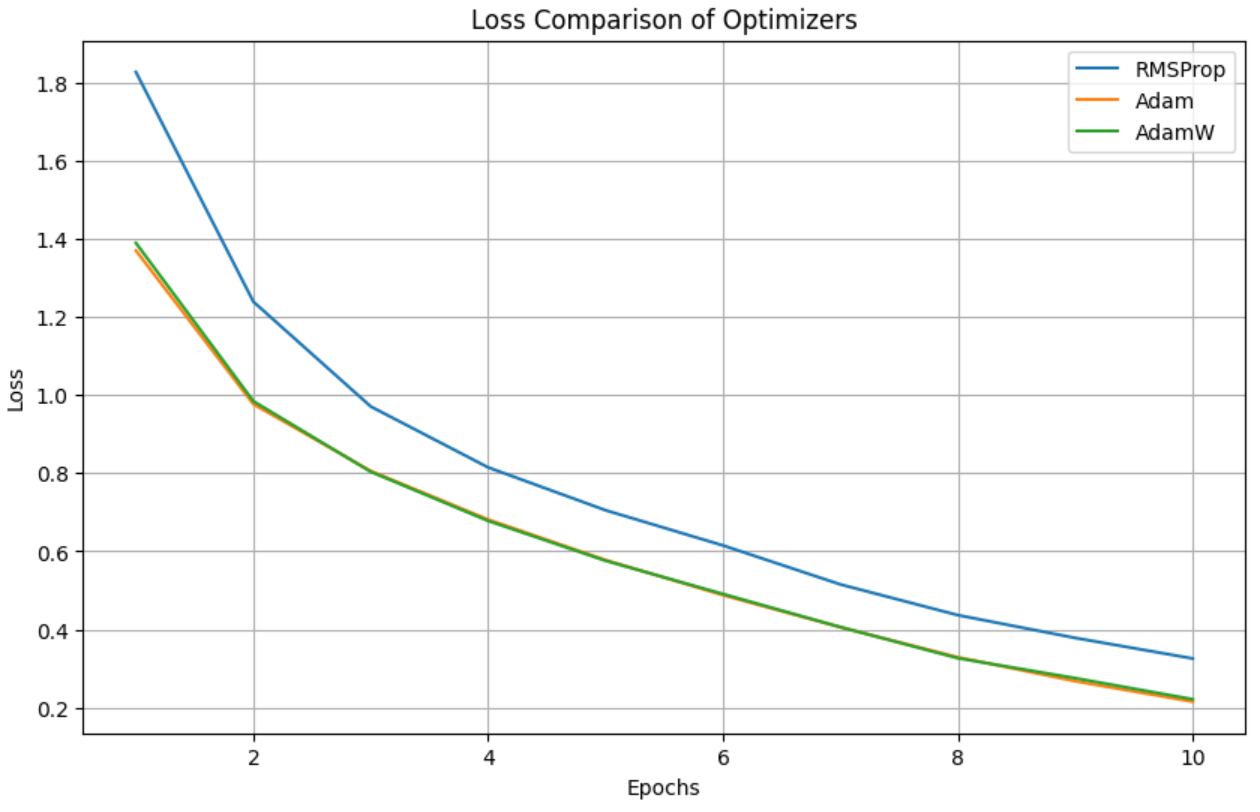
해석 및 관찰
- 초기 학습 속도
- Adam과 AdamW는 초기 학습에서 빠르게 손실(loss)을 감소시키는 모습을 보여준다.
- 이는 Adam과 AdamW가 1차 모멘트(기울기의 평균 방향)와 2차 모멘트(기울기의 크기)를 모두 고려하여 초기 학습률을 적응적으로 조정하기 때문이다.
- 반면, RMSProp는 초기 손실 감소 속도가 상대적으로 느리다. 이는 RMSProp가 2차 모멘트만을 고려하여 학습률을 조정하기 때문이다.
- 후반 수렴 속도
- AdamW는 학습 후반부에서도 안정적으로 손실을 줄이는 경향을 보여준다.
- Adam은 AdamW와 거의 비슷한 성능을 보이지만, 아주 미세하게 더 느린 수렴을 보일 수 있다.
- RMSProp는 꾸준히 손실을 줄이지만, Adam 계열보다는 다소 비효율적으로 보인다.
- 최종 손실값
- Adam과 AdamW가 거의 비슷한 최종 손실값에 도달하고, RMSProp은 여전히 더 높은 손실값을 유지한다.
- 이는 AdamW와 Adam이 학습률 조정에서 더 세밀하게 동작하기 때문이다.
- 일반화에 대한 의문
- 이 그래프는 훈련 손실(training loss)만을 보여준다.
최종적으로 모델의 일반화 성능(Generalization)을 확인하려면 테스트 데이터셋에서의 성능을 측정해야 한다. - AdamW는 일반적으로 Weight Decay(가중치 감쇠)를 명확히 적용하므로, 과적합 방지 및 일반화 성능 향상에 더 유리할 가능성이 있다.
- 이 그래프는 훈련 손실(training loss)만을 보여준다.
이상으로 Adam 에 대한 내용을 마치겠습니다.
감사합니다
'딥러닝 (Deep Learning) > [04] - 학습 및 최적화' 카테고리의 다른 글
| TensorRT 개념 및 이해 (1) | 2025.03.27 |
|---|---|
| PyTorch(.pt) vs ONNX 무엇이 다르고, 왜 ONNX 추론이 더 빠를까? (2) | 2025.03.14 |
| [Optimizer] - 초기 optimizer 이해 [1] (3) | 2024.12.28 |
| Pseudo 라벨링(Pseudo Labeling)이란 무엇인가? (0) | 2024.11.24 |
| 딥러닝 학습률(Learning Rate) 종류와 설정 방법 (2) | 2024.11.17 |
