활성화함수 (Activation funtion)

1. Sigmoid 함수

수식
\begin{flalign*}
   \sigma(z) = \frac{1}{1 + e^{-z}} &&
\end{flalign*}  ​

 

장점

• 출력이 [0, 1] 범위로 제한되어 있습니다.

단점

1. Vanishing Gradient
   Sigmoid 함수의 기울기는 입력값이 크거나 작을 때 0에 가까워집니다. 이로 인해 역전파 과정에서 기울기가 0으로 변할 수 있습니다. 이는 다음 단계로의 그라디언트가 0이 되어 학습이 제대로 이루어지지 않는 문제를 일으킵니다. 수식으로 표현하면,
   \[ \frac{d\sigma(x)}{dx} = \sigma(x) \cdot (1 - \sigma(x)) \]
   기울기가 0에 가까워질 수 있습니다.
2. Non-zero-centered Output
   Sigmoid 함수의 출력값이 항상 양수이므로, 네트워크의 각 층이 항상 같은 방향으로 기울기를 가지게 되어, 비효율적인 학습을 초래할 수 있습니다.
   Gradient 부호가 변하지 않아서 특정 방향으로만 업데이트가 된다.
   x,y 그래프에서 (x가 양수, y가 양수) , (x 음수, y 음수) 방향으로만 업데이트가 된다는 것이다.
   더 좋은 방향(그레디언트)로 갈 수 있는데 특정 방향으로만 업데이트 하니깐 비효율적이다.

예제 코드

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

 

---

2. Tanh 함수

수식
\[ \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \] ​

장점

• 출력이 [-1, 1] 범위로 제어되어 있어, zero-centered 특성을 가집니다.

단점

• Vanishing Gradient
  Tanh 함수도 입력값이 크거나 작을 때 기울기가 0에 가까워지며, 이는 sigmoid와 유사한 vanishing gradient 문제를 일으킬 수 있습니다

예제코드

import numpy as np

def tanh(x):
    return np.tanh(x)

 

---

3. ReLU (Rectified Linear Unit) 함수

수식
\[
\text{ReLU}(x) = \max(0, x)
\]

장점

• Vanishing Gradient 문제 없음
  입력값이 0보다 클 때 기울기가 항상 1로 유지되어, vanishing gradient 문제를 해결합니다.
• 계산 효율성
  함수가 매우 간단하고 미분 시 1로 유지되므로 연산이 효율적입니다.

단점

• Not Zero-centered Output
  출력값이 음수일 경우 완전히 0이 되며, 따라서 출력값이 0을 중심으로 하지 않습니다.
• Dead ReLU 문제
  입력이 0 이하일 때 기울기가 0이 되므로, 이 부분에서 학습이 제대로 이루어지지 않습니다.
  
  

예제코드

import numpy as np

def relu(x):
    return np.maximum(0, x)

---

4. Leaky ReLU (Leaky Rectified Linear Unit)

특징

• Dead ReLU 문제 해결:
  • ReLU 함수는 입력이 0 이하일 때 기울기가 0이 되어 학습이 이루어지지 않는 문제가 있습니다. Leaky ReLU는 이 문제를 해결하기 위해, 입력이 0 이하일 때도 작은 기울기 값을 갖도록 설계되었습니다.
  • 수식:
    \[ \text{Leaky ReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases} \] ​
    여기서 α 는 작은 상수 (예: 0.01)입니다.

단점

• 추가적인 하이퍼파라미터 비용:
  • α\alphaα 값(기울기 조정 상수)을 설정해야 하며, 이로 인해 하이퍼파라미터 조정이 필요합니다.
    
    
    

예제코드

import numpy as np

def leaky_relu(x, alpha=0.01):
    return np.where(x > 0, x, alpha * x)

 

---

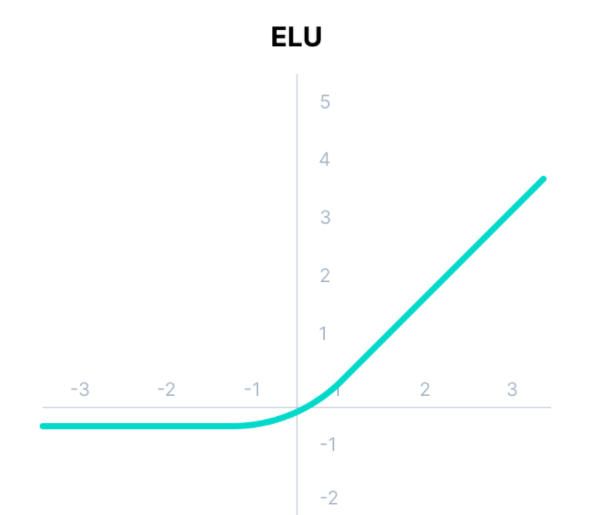
5. ELU (Exponential Linear Unit)

특징

• 음수 부분에서 기울기 변동
  • ELU는 입력이 음수일 때 기울기가 0이 아닌 작은 값을 갖도록 설계되어 vanishing gradient 문제를 완화합니다.
  • 수식:
    \[ \text{ELU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha \left(e^x - 1\right) & \text{if } x \leq 0 \end{cases} \] ​
    여기서 α 는 양수 상수입니다.

단점

• 계산 복잡성
  • exp() 연산이 필요하여 계산 비용이 상대적으로 높습니다.

 

예제코드

import numpy as np

def elu(x, alpha=1.0):
    return np.where(x > 0, x, alpha * (np.exp(x) - 1))